PAT(A) 1123. Is It a Complete AVL Tree (30)

日期: 2018年3月12日 14:05 作者: 胡城北 分类: PAT甲级 标签: PAT 阅读(1360) 评论(0)

原题目：

原题链接：https://www.patest.cn/contests/pat-a-practise/1123

1123. Is It a Complete AVL Tree (30)

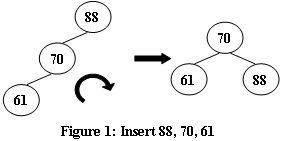
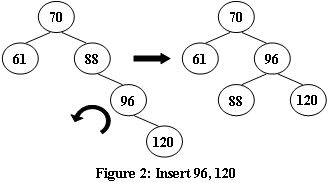
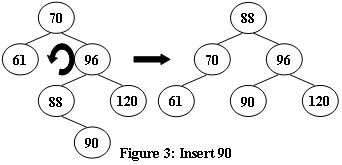
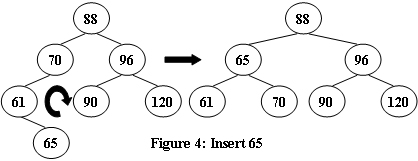
An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.

Now given a sequence of insertions, you are supposed to output the level-order traversal sequence of the resulting AVL tree, and to tell if it is a complete binary tree.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (<= 20). Then N distinct integer keys are given in the next line. All the numbers in a line are separated by a space.

Output Specification:

For each test case, insert the keys one by one into an initially empty AVL tree. Then first print in a line the level-order traversal sequence of the resulting AVL tree. All the numbers in a line must be separated by a space, and there must be no extra space at the end of the line. Then in the next line, print "YES" if the tree is complete, or "NO" if not.

Sample Input 1: 5 88 70 61 63 65 Sample Output 1: 70 63 88 61 65 YES Sample Input 2: 8 88 70 61 96 120 90 65 68 Sample Output 2: 88 65 96 61 70 90 120 68 NO

题目大意

建立一个平衡二叉树，层序输出节点，并判断是否是完全二叉树

解题报告

  1. 根据节点依次插入树内。
  2. 判断是否平衡，依据插入方式进行左旋或者右旋。
  3. 难点就在于左旋右旋以及如何判断旋转。

代码

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
/*
* Problem: 1123. Is It a Complete AVL Tree (30)
* Author: HQ
* Time: 2018-03-12
* State: Done
* Memo: 平衡二叉树、完全二叉树
*/
#include "iostream"
#include "algorithm"
#include "queue"
using namespace std;

typedef struct Node {
    int data = -1;
    struct Node * left = NULL;
    struct Node *  right = NULL;
};

int N;

int deap(struct Node * root) {
    if (root == NULL)
        return 0;
    return max(deap(root->left), deap(root->right)) + 1;
}

void leftRotate(struct Node * &root) {
    struct Node *  temp;
    temp = root;
    root = root->right;
    temp->right = root->left;
    root->left = temp;
}

void rightRotate(struct Node *  &root) {
    struct Node *  temp;
    temp = root;
    root = root->left;
    temp->left = root->right;
    root->right = temp;
}

void insert(struct Node* &root, int x,int &pos) { // pos 0:本位插入，1左边，2右边
    if (root->data == -1) {
        root->data = x;
        return;
    }
    int p = 0;
    if (x < root->data) {
        if (root->left == NULL)
            root->left = new Node;
        pos = 1;
        insert(root->left, x,p);
    }
    else {
        if (root->right == NULL)
            root->right = new Node;
        pos = 2;
        insert(root->right, x,p);
    }
    int l = deap(root->left);
    int r = deap(root->right);
    if (l - r > 1) {
        if (p == 1) {
            rightRotate(root);
        }
        if (p == 2) {
            leftRotate(root->left);
            rightRotate(root);
        }
    }
    if (r - l > 1) {
        if (p == 1) {
            rightRotate(root->right);
            leftRotate(root);
        }
        if (p == 2) {
            leftRotate(root);
        }
    }
}


int main() {
    struct Node * root = new Node;
    cin >> N;
    int x;
    for (int i = 0; i < N; i++) {
        cin >> x;
        int pos = 0;
        insert(root, x, pos);
    }
    queue<struct Node*> q;
    struct Node * temp;
    q.push(root);
    bool first = true;
    bool end = false, flag = true;
    while (!q.empty()) {
        temp = q.front();
        q.pop();
        if (end && (temp->left != NULL || temp->right != NULL))
            flag = false;
        if (temp->left == NULL && temp->right != NULL)
            flag = false;
        if (temp->left != NULL)
            q.push(temp->left);
        else
            end = true;
        if (temp->right != NULL)
            q.push(temp->right);
        else
            end = true;
        if (first) {
            cout << temp->data;
            first = false;
        }else
            cout << " " << temp->data;
    }
    cout << endl << (flag ? "YES" : "NO") << endl;
    system("pause");
}
« 上一篇
下一篇 »
发表评论:
评论列表:
近期文章
分类
标签
热门